Reachable Coverage: Estimating Saturation in Fuzzing [ICSE 2023]

image-20251120090656519

精确估计 Fuzzing 在每个目标程序中的可达元素个数(边, 分支, 块等) 是不可判定问题, 因此需要使用统计学方法来估计一个近似值, 依次判断 fuzzer 的有效性. 论文评估了多个 SOTA 估计器在 fuzzing 上估计可达元素个数的效果, 并提出应该用 Bernoulli-product model 来建模 fuzzing campaign 的 N 个输入与覆盖元素 S 之间的关系, 然后用 Chao, ICE, JK 等系列估计器来估计目标程序的可达覆盖元素个数的下界, 而非精确值.

Methods

image-20251124160055131

Evaluation

RQ.1 (Ground truth). For programs where we know the reachable coverage, how do existing species richness estimators perform as approximators of reachable coverage?

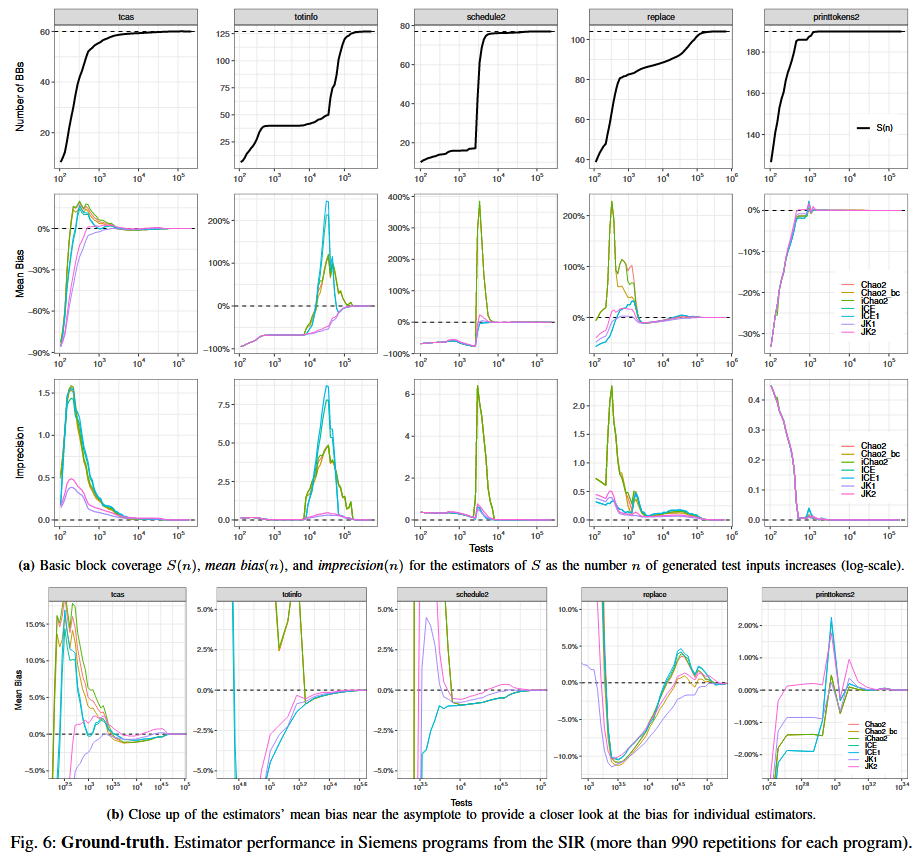
image-20251124220743922

在最初的“预热”阶段之后, 除 iChao2 以外, 所有估计器对可达覆盖率的估计平均来说都是偏高的, 但偏差控制在 15% 以内. 所有估计器在渐近意义上都是一致的, 也就是说, 随着样本数 $n$ 的增加, 它们的偏差大小会逐渐减小. 对于那些规模足够小、使得其渐近极限 (真实可达覆盖上限) 可以被精确知道的程序, Jackknife 估计器的表现最好.

RQ.2 (Real world). For real-world programs, how do existing estimators perform as approximators of reachable coverage?

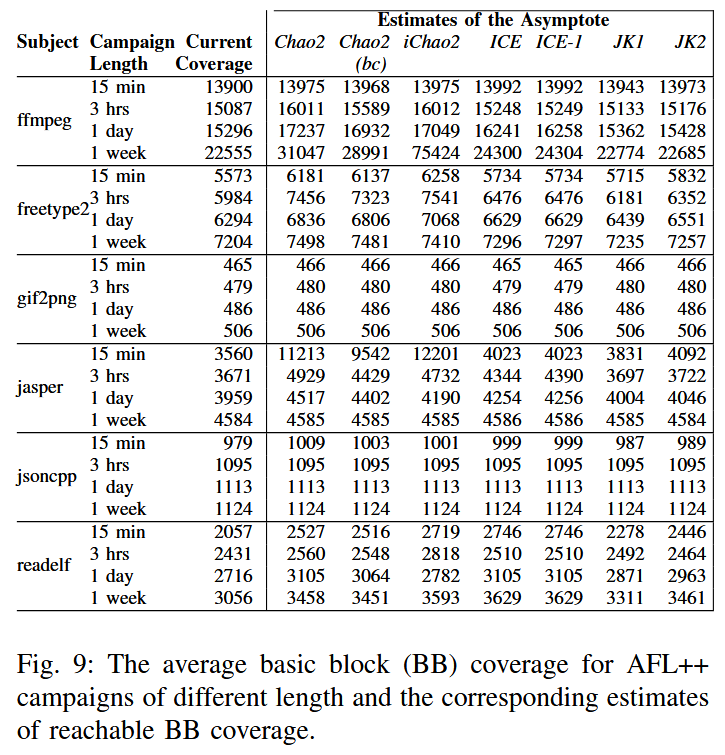
image-20251124221019711

所有被评估的估计器都会预测出虚假的峰值: 在大多数情况下, 即使达到它们所预测的可达覆盖上限之后, 依然还能取得更多的覆盖. 所有估计器都对 $S$ 做出了偏低的估计.

RQ.3 (Bootstrapped ground truth). For real-world programs, where we “force” a known asymptote by bootstrapping, how do existing estimators perform?

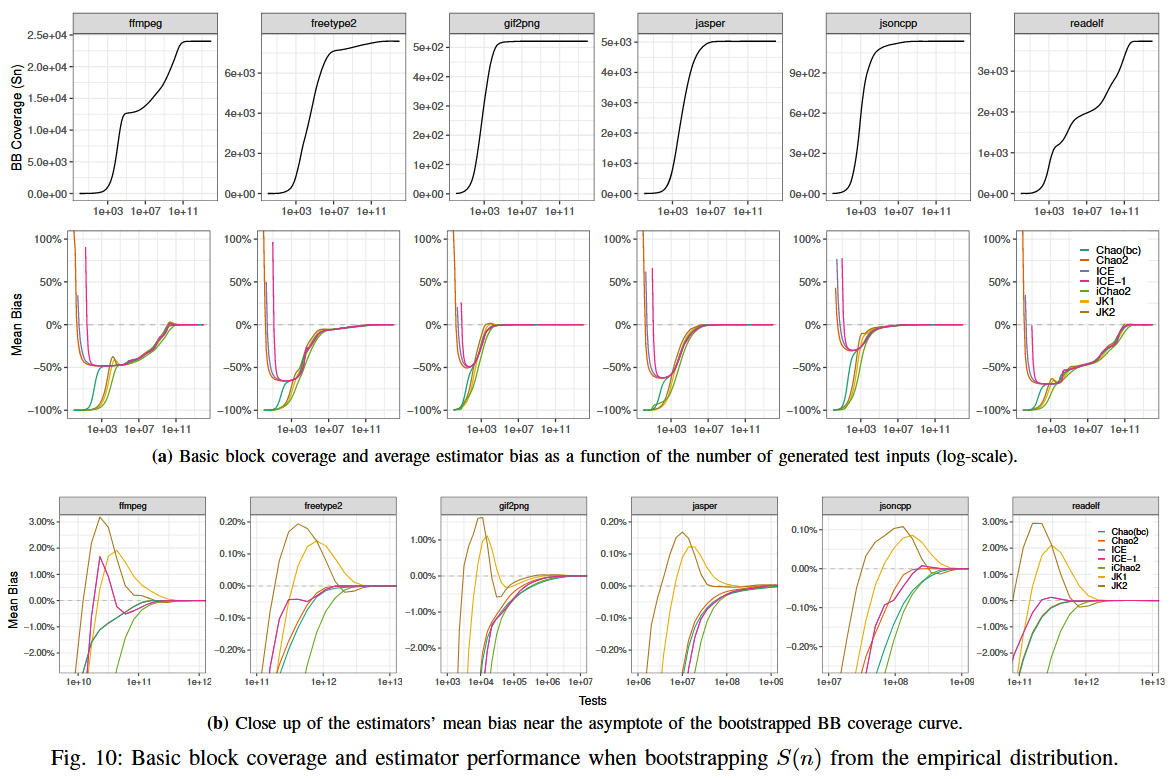
image-20251124221421826

在实验活动 (campaign) 的早期阶段, 由于在对数时间尺度上看不出任何明显的渐近趋势 (asymptote) , 所有估计器都会产生虚假的峰值预测 (与 RQ.2 中的情况相同) . 然而, 随着实验持续时间的增加, 这种系统性的负偏差会逐渐减弱, 从而体现出所有估计器的渐近一致性. 在经历了最初的“预热” (burn-in) 阶段之后, 所有估计器对可达覆盖率的预测都能控制在 ±3% 的误差范围之内. 在所有被评估的估计器中, Jackknife 系列的表现最好 (与 RQ.1 中的结论一致) .

Conclusions

对于静态分析, 我们发现, 即便是工业界和学术界开发的最先进工具, 在可达覆盖率上也存在严重的高估或低估. Fuzz-Introspector [16] 由 Google 开发, 用来衡量 fuzzer 的有效性；SVF [51] 则由 Sui 课题组开发, 目标是在过程间可达性分析中最大化精度. 然而, 它们给出的近似结果都难以被可靠地解释. 实际上, 这些结果具体到底偏差多大很难确定, 而且也无法仅仅通过“把分析跑久一点”来动态改进精度. 对于估计方法, 我们发现, 与其他最先进的估计器相比, Jackknife 估计器 [15] 在偏差和方差方面都最小. 一阶 Jackknife (JK1) 的计算方式是: 将已覆盖的代码元素数量与只出现一次的元素数量相加, 得到估计值 S^=S(n)+f1(n)\hat{S} = S(n) + f_1(n). 在实际可达覆盖率 SS 真正被达到之前的 1–2 个数量级区间内, 估计值 S^\hat{S} 与真实 SS 的平均差异始终保持在 SS 的 ±3%\pm 3\% 之内. 举例来说, 如果真实的 SS 需要 30 天才能达到, 那么 Jackknife 估计器大约在第 3 天左右就能给出 S±3%S \pm 3\% 这样精度的估计. 然而, 在不知道 SS 真值的情况下, 我们发现, 在 fuzzing 活动的早期阶段, 所有估计器都会预测出虚假的峰值: 当达到估计的可达覆盖率 S^\hat{S} 时, 总是还可以获得更多覆盖, 即 S>S^S > \hat{S}. 在假定“分析是完全的”的前提下, 静态分析最多只能给出 SS 的一个上界 (除非验证问题在实践中是可行的) . 与此相反, 这些被评估的最先进估计器只能给出一个下界. 正如本文所示, 在这两种情况下, 我们都很难精确判断这两类方法分别在多大程度上高估或低估了 SS. 不过, 与静态分析不同的是, 估计方法始终可以通过延长 fuzzing 活动的时间来不断改善这个下界. 在实践中, 我们建议同时使用这两种方法.

References

[16] O. Chang, N. Emamdoost, A. Korczynski, and D. Korczynski, “Introducing fuzz introspector, an openssf tool to improve fuzzing coverage,” https://openssf.org/blog/2022/06/09/ introducing-fuzz-introspector-an-openssf-tool-to-improve-fuzzing-coverage/, accessed: 2022-08-15.

[51] Y. Sui and J. Xue, “Svf: interprocedural static value-flow analysis in llvm,” in Proceedings of the 25th international conference on compiler construction. ACM, 2016, pp. 265–266.

results matching ""

    No results matching ""